Probabilidad y estadística.
El análisis genético de la herencia mendeliana normalmente recae en la interpretación de valores numéricos obtenidos directamente como observaciones en una progenie. Estos datos se cuantifican como proporciones de clases fenotípicas.Al aplicar varios métodos estadísticos el genetista puede: (1) juzgar cuando los datos numéricos se ajustan o no al patrón hereditario esperado, (2) calcular la probabilidad de que ocurra un evento una vez que se ha establecido el patrón, (3) juzgar estadísticamente cuando existe una base genética en el patrón de transmisión hereditaria bajo estudio.
En los patrones de herencia mendeliana, que se deben a dominancia completa de un alelo sobre otro, se puede calcular la proporción de los fenotipos mediante el binomio (3:1)n donde n es el número de genes involucrados, y, mediante el trinomio (1:2:1)n el número de genotipos esperados.
El teorema del binomio permite predecir la frecuencia de genotipos y fenotipos involucrados en los análisis de las cruzas y de los árboles genealógicos o de los pedigríes. La expresión del teorema del binomio es útil para situaciones en las cuales una o más alternativas pueden ocurrir al azar para cada evento independiente, tales como: macho o hembra, cara o cruz de una moneda.
En el binomio (a+b)n a representa la probabilidad de que ocurra una alternativa y b de que ocurre la otra alternativa que es excluyente del mismo evento; n representa los eventos independientes o los individuos. Si se trata de dos eventos independientes, entonces n = 2 y la probabilidad para todas las combinaciones posibles es (a+b)2 ; para tres eventos independientes es (a+b)3 , etc. (Tabla 3.3).
Para desarrollar el binomio de Newton: el exponente de a pierde uno en cada progresión y el de b lo gana; el coeficiente se obtiene multiplicando el coeficiente del primero por el exponente del primer término dividido entre el término en cuestión (Fig. 3.9). Con los coeficientes que preceden a cada expresión del binomio se construye el triángulo de Pascal (Fig. 3.10). En donde todos los valores distintos a 1 se obtienen sumando los dos números que se encuentran directamente encima de ellos.
Si aplicamos la distribución binomial y queremos, por ejemplo, conocer en una familia con n número de hijos la probabilidad de que sean de un sexo o de otro, entonces considerando que cada sexo tiene una probabilidad independiente de ½, (a = 1/2 y b = 1/2), entonces se puede seleccionar el término apropiado para calcular el valor numérico de una frecuencia con una combinación particular, considerando que a = ♂ y b = ♀ (Tabla 3.4).
La distribución binomial puede aplicarse también para calcular la probabilidad de otras variables discretas como las caras de una moneda. Así si lanzo al aire una moneda existe la misma probabilidad (1/2) de que al caer al suelo caiga cara o caiga cruz. Si la lanzo cien veces existe la probabilidad teórica de que caiga 50 veces cara y 50 veces cruz. Si se lanzan al aire dos monedas simultáneamente, cien veces, éstas se comportan independientemente una de la otra, por probabilidad se espera que caigan ¼ cara cara ½ cara cruz y ¼ cruz cruz. Distribución que es paralela a la segregación de genotipos (1:2:1) en una cruza monohíbrida.
La proporción es el promedio de resultados esperados cuando ocurren eventos independientes (Fig.3.12). Por lo que si dos o más eventos son independientes, la probabilidad de que ocurran juntos es, de acuerdo a ley de probabilidades del producto, el producto de sus probabilidades por separado.
Ji cuadrada. La prueba de bondad del ajuste o estimación de la validez de una hipótesis para variables discretas se denomina prueba de ji cuadrada. Se basa en los acontecimientos observados y el cálculo de los esperados bajo una prueba de hipótesis, llamada hipótesis alternativa (HA). La hipótesis nula (Ho) establece que no existen diferencias entre los valores observados y los esperados. De modo que si se acepta la Ho, se acepta que las diferencias son debidas al azar. Si se rechaza la Ho, entonces las diferencias no son debidas al azar, y se acepta la HA . Esta prueba estadística toma en cuenta:
- el tamaño de la muestra. A medida que éste aumenta, la desviación respecto de la proporción esperada disminuye, por lo que en una muestra grande el impacto sobre las desviaciones al azar disminuye.
- la desviación de la proporción esperada.
- los grados de libertad se calculan con base en el número de clases de fenotipos, es decir, n –1
- del tamaño total de la muestra se obtienen los valores teóricos (esperados), así que para dos clases.
Imagen de: https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhME_3zut-IoMczGBDl87DWEOdjiZSEmBqoRDBfCXNTVZjywmPM2-3OH-oqy4D4-P7Jr08sV9eUWfh7XGSdap_lKIf_x3D04TjQr5WpSF212DHB85QhvdAAwOnpkfAHBVIVicSHPrSMrEc/s1600/formula.jpg







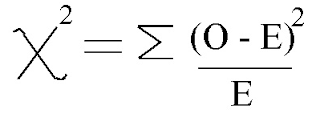





%206.41.29%E2%80%AFp.m..png)
.png)

Excelente informacion y ejemplos. gracias
ResponderBorrarGracias. Me ha servido mucho este artículo para dar mis clases.
ResponderBorrar